Numeri float

La conversione di numeri da base decimale a binario è una competenza fondamentale in informatica, specialmente quando si tratta di rappresentare numeri in virgola mobile, o float. Oggi, ci concentreremo sulla conversione di un numero decimale, 205.125, in un numero binario float.

I numeri float sono rappresentati in un formato standardizzato, tipicamente il formato IEEE 754, che suddivide il numero in tre parti: il segno, l'esponente e la mantissa.

La conversione in binario coinvolge sia la conversione della parte intera che quella frazionaria del numero. Vediamo come si svolge questo processo passo dopo passo.

Conversione della Parte Intera

Iniziamo convertendo la parte intera del numero, 205, in binario.

La conversione della parte intera si fa dividendo continuamente il numero per 2 e registrando i resti fino a quando il quoziente diventa 0.

Convertendo 205 in binario:

205 diviso 2 è 102 con resto 1

102 diviso 2 è 51 con resto 0

51 diviso 2 è 25 con resto 1

25 diviso 2 è 12 con resto 1

12 diviso 2 è 6 con resto 0

6 diviso 2 è 3 con resto 0

3 diviso 2 è 1 con resto 1

1 diviso 2 è 0 con resto 1

Scrivendo i resti in ordine inverso, otteniamo 11001101, che è 205 in binario.

Conversione della Parte Frazionaria

Ora passiamo alla parte frazionaria del nostro numero, 0.125.

Per convertire la parte frazionaria, moltiplichiamo la frazione per 2 e registriamo la cifra prima della virgola, poi continuiamo con la parte frazionaria del risultato fino a raggiungere una risoluzione accettabile o un pattern ricorrente.

Convertendo 0.125 in binario:

0.125 2 = 0.25, quindi prendiamo 0 e continuiamo con 0.25

0.25 2 = 0.5, quindi prendiamo 0 e continuiamo con 0.5

0.5 2 = 1.0, quindi prendiamo 1 e non abbiamo più una parte frazionaria

Quindi, 0.125 in binario è 0.001

Riunire le Parti e Formattare come Float

Abbiamo convertito la parte intera e frazionaria separatamente. La parte intera è 11001101 e la parte frazionaria è .001. Unendo le due parti otteniamo 11001101.001 in binario.

Ora, dobbiamo rappresentare questo numero nel formato float. Per farlo, dobbiamo normalizzare il numero, spostare la virgola dopo il primo bit 1 e usare la notazione scientifica binaria.

Normalizziamo 11001101.001:

Il numero diventa 1.1001101001 × 2⁷ perché abbiamo spostato la virgola di 7 posizioni verso sinistra.

Quindi, abbiamo:

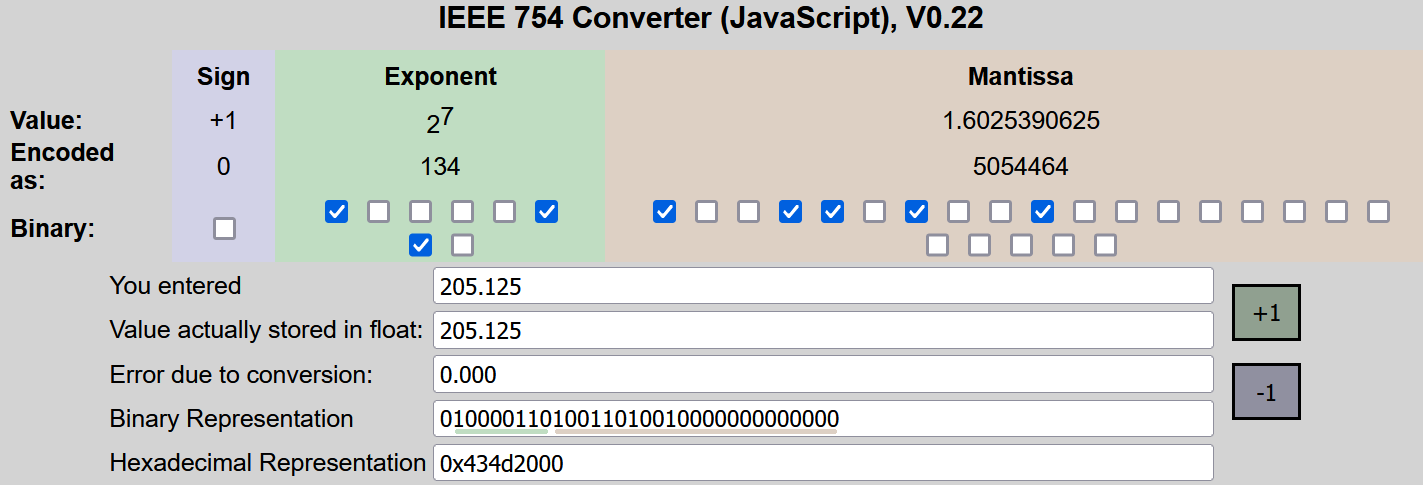
Segno = 0 (perché il numero è positivo)

Esponente = 7 (ma dobbiamo applicare il bias. Per il formato float IEEE 754 a 32 bit, il bias è 127. Quindi, l'esponente memorizzato sarà 7 + 127 = 134, che è 10000110 in binario.)

Mantissa = Parte dopo la virgola di 1.1001101001, cioè 1001101001 (possono essere necessari alcuni zeri alla fine per riempire la lunghezza della mantissa per il formato specifico, in questo caso, 23 bit totali per la mantissa nel formato IEEE 754 a 32 bit).

Unendo queste parti, otteniamo la rappresentazione binaria float di 205.125.

Il Bias

il concetto di "bias" nella rappresentazione dei numeri in virgola mobile (float) è un punto cruciale per capire come i computer rappresentano e gestiscono i numeri reali. Il bias viene usato nel contesto dell'esponente in formati come il formato IEEE 754 per i numeri float:

1. Rappresentazione Uniforme:

   • Esponente con e senza Bias: In un sistema di numerazione in virgola mobile, l'esponente può essere positivo o negativo. Senza bias, dovremmo usare un bit per il segno dell'esponente, e il resto dei bit per rappresentare il valore assoluto dell'esponente. Tuttavia, questo approccio introduce complessità quando si eseguono confronti o si ordinano i numeri in virgola mobile.
   • Uso del Bias: Aggiungendo un bias all'esponente, possiamo rappresentare l'esponente sempre come un numero non negativo (cioè, un numero senza segno). Questo rende molto più semplice il confronto tra numeri in virgola mobile, perché possiamo confrontare le loro rappresentazioni binarie direttamente, come se fossero interi non segnati.

2. Rappresentazione di Zero, Numeri Molto Piccoli e Numeri Negativi:

   • Zero e Denormalizzati: L'uso del bias permette anche una rappresentazione efficiente dello zero e di numeri molto piccoli, detti numeri denormalizzati. Se non usassimo il bias, dedicare una rappresentazione specifica allo zero e ai numeri molto piccoli sarebbe più complesso.
   • Numeri Negativi: Con il bias, possiamo utilizzare la stessa rappresentazione binaria sia per numeri positivi sia per numeri negativi, cambiando solo il bit di segno. Questo semplifica le operazioni aritmetiche tra numeri in virgola mobile.

3. Ottimizzazione dell'Utilizzo dello Spazio di Memorizzazione:

   • Utilizzo Efficace dei Bit: Usando il bias, possiamo rappresentare un intervallo più ampio di numeri usando lo stesso numero di bit per l'esponente. Questo è perché possiamo sfruttare tutti i possibili valori che i bit dell'esponente possono assumere.

4. Standardizzazione e Convenienza nel Calcolo:

   • IEEE 754: L'adozione del bias è parte dello standard IEEE 754 per la rappresentazione dei numeri in virgola mobile. Questo standard garantisce che i numeri in virgola mobile siano rappresentati e gestiti in modo coerente tra diverse piattaforme e architetture hardware, facilitando lo sviluppo e la portabilità del software.

In sintesi, l'uso del bias nell'esponente dei numeri float è una scelta progettuale che aiuta a semplificare le operazioni, ottimizzare l'uso dello spazio di memorizzazione, e garantire la compatibilità e la standardizzazione tra differenti sistemi e architetture. Queste sono le ragioni fondamentali per cui il bias è una componente critica nella rappresentazione dei numeri in virgola mobile nei computer.

Conclusione

Convertire numeri da decimale a binario, specialmente per i float, richiede attenzione ai dettagli e comprensione dei formati binari. Attraverso questo processo, abbiamo trasformato 205.125 in una forma che un computer può comprendere e rappresentare internamente.

La rappresentazione in binario di numeri float è essenziale per calcoli scientifici, grafica computerizzata e molte altre applicazioni dove la precisione e la rappresentazione dei numeri è cruciale.

Ricordate che la pratica rende perfetti, quindi vi incoraggio a provare con altri numeri per affinare la vostra comprensione di questo processo!