La notazione esadecimale

La notazione esadecimale, conosciuta anche come sistema base-16, è un sistema numerico posizionale che utilizza sedici simboli distinti per rappresentare numeri. Questi simboli sono 0-9 e A-F. In questa lezione, ci addentreremo nel fascino di questo sistema numerico e vedremo come e perché viene utilizzato nella tecnologia moderna, soprattutto in informatica.

Che cosa è un sistema numerico posizionale?

Prima di entrare nei dettagli della notazione esadecimale, è essenziale capire cosa intendiamo con "sistema numerico posizionale". La maggior parte di noi è familiare con il sistema decimale, che è un sistema base-10. Nel sistema decimale, ogni posizione in un numero ha un valore basato su potenze di 10. Ad esempio, nel numero 235, il "5" è nella posizione delle unità, il "3" in quella delle decine e il "2" in quella delle centinaia.

235 = 2(10^2) + 3(10^1) + 5(10^0) = 200 + 30 + 5 = 235

Allo stesso modo, in un sistema numerico posizionale, ogni posizione ha un valore basato su potenze della sua base. La notazione esadecimale, essendo base-16, usa potenze di 16 per determinare il valore di ciascuna posizione.

I simboli nel sistema esadecimale

Nel sistema decimale, utilizziamo i numeri da 0 a 9 per rappresentare valori. Ma nel sistema esadecimale, abbiamo bisogno di sedici simboli distinti. Per questo, oltre ai numeri da 0 a 9, utilizziamo le lettere da A a F per rappresentare i valori da 10 a 15.

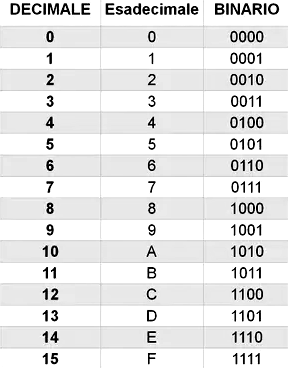
0-9 nel sistema esadecimale rappresentano i valori da 0 a 9. A-F rappresentano i valori da 10 a 15.

Conversione da binario ad esadecimale:

Convertire direttamente da binario a esadecimale è relativamente semplice una volta compreso il metodo. La chiave è ricordare che ogni cifra esadecimale può rappresentare esattamente 4 cifre binarie.

1) Convertiamo il numero binario '11010101' in esadecimale:

1. Dividi il numero binario in gruppi di 4 cifre partendo dalla destra. Se l'ultimo gruppo (a sinistra) ha meno di 4 cifre, aggiungi zeri davanti per completarlo. In questo caso, otteniamo: '1101' e '0101'.
2. Converti ogni gruppo in esadecimale:
   • '1101' in binario è 13 in decimale, che è 'D' in esadecimale.
   • '0101' in binario è 5 in decimale, che resta '5' in esadecimale.
3. Combina i gruppi convertiti per ottenere il numero esadecimale completo: 'D5'.

'11010101' in binario si converte in 'D5' in esadecimale.

2) Convertiamo il numero binario '101010111001' in esadecimale:

1. Dividi il numero binario in gruppi di 4 cifre partendo dalla destra. Otteniamo: '1010', '1011' e '1001'.
2. Converti ogni gruppo in esadecimale:
   • '1010' in binario è 10 in decimale, che è 'A' in esadecimale.
   • '1011' in binario è 11 in decimale, che è 'B' in esadecimale.
   • '1001' in binario è 9 in decimale, che resta '9' in esadecimale.
3. Combina i gruppi convertiti per ottenere il numero esadecimale completo: 'AB9'.

'101010111001' in binario si converte in 'AB9' in esadecimale.

Questi esempi dovrebbero illustrare chiaramente il processo di conversione da binario a esadecimale. Utilizzando questo metodo, puoi convertire qualsiasi sequenza binaria in formato esadecimale.

Quando si divide una stringa binaria in gruppi da 4 bit, si parte da destra e, se i bit della stringa non sono multipli di 4, si aggiungono degli 0 a sinistra.

Conversione da esadecimale a binario

1) Convertiamo il numero esadecimale 'B4' in binario:

1. Prendi la cifra esadecimale più a sinistra, 'B', che corrisponde a 11 in decimale. La rappresentazione binaria di 11 è '1011'.
2. Prendi la cifra esadecimale successiva, '4', che corrisponde a 4 in decimale. La rappresentazione binaria di 4 è '0100'.
3. Combina le rappresentazioni binarie per ottenere il numero binario completo: '10110100'.

'B4' in esadecimale si converte in '10110100' in binario.

2) Convertiamo il numero esadecimale '7F' in binario:

1. Prendi la cifra esadecimale più a sinistra, '7', che corrisponde a 7 in decimale. La rappresentazione binaria di 7 è '0111'.
2. Prendi la cifra esadecimale successiva, 'F', che corrisponde a 15 in decimale. La rappresentazione binaria di 15 è '1111'.
3. Combina le rappresentazioni binarie per ottenere il numero binario completo: '01111111'.

'7F' in esadecimale si converte in '01111111' in binario.

Utilizzando questo metodo, puoi convertire qualsiasi cifra o sequenza esadecimale in formato binario.

Convertire dal sistema decimale all'esadecimale

Una delle prime abilità che dovremmo acquisire è come convertire numeri dal sistema decimale all'esadecimale.

Convertiamo il numero decimale 439 in esadecimale:

1. Dividiamo 439 per 16. Il quoziente è 27 e il resto è 7.
2. Il resto, 7, sarà la cifra più a destra del nostro numero esadecimale. Quindi, per ora, abbiamo... 7.
3. Prendiamo il quoziente, 27, e dividiamolo nuovamente per 16. Il quoziente ora è 1 e il resto è 11. Nell'esadecimale, 11 è rappresentato dalla lettera 'B'.
4. Ora abbiamo... B7.
5. Il nuovo quoziente è 1. Poiché 1 è minore di 16, diventa la nostra prossima (e ultima) cifra.
6. Ora abbiamo il nostro numero in esadecimale ... 1B7 leggendo dal basso verso l'alto.

Il numero 439 in decimale si converte in 1B7 in esadecimale.

Convertiamo il numero decimale 685 in esadecimale:

1. Dividiamo 685 per 16. Il quoziente è 42 e il resto è 13. Nell'esadecimale, 13 è rappresentato dalla lettera 'D'.
2. Il resto, 'D', sarà la cifra più a destra del nostro numero esadecimale. Quindi, per ora, abbiamo... D.
3. Prendiamo il quoziente, 42, e dividiamolo nuovamente per 16. Il quoziente ora è 2 e il resto è 10. Nell'esadecimale, 10 è rappresentato dalla lettera 'A'.
4. Ora abbiamo... AD.
5. Il nuovo quoziente è 2. Poiché 2 è minore di 16, diventa la nostra prossima (e ultima) cifra.
6. Ora abbiamo... 2AD

Il numero 685 in decimale si converte in 2AD in esadecimale.

Convertire dall'esadecimale al decimale

Ora, vediamo come convertire un numero da esadecimale a decimale. Convertiamo '4F3' in esadecimale al suo equivalente decimale:

1. Prendiamo la cifra più a destra, '3', e moltiplichiamo per \(16^0\) (cioè 1). 3 × 1 = 3.
2. Passiamo alla cifra successiva a sinistra, 'F'. 'F' in decimale è 15. Moltiplichiamo per \(16^1\) (cioè 16). 15 × 16 = 240.
3. Ora, prendiamo la cifra più a sinistra, '4', e moltiplichiamo per \(16^2\) (cioè 256). 4 × 256 = 1024.
4. Sommiamo tutti i risultati ottenuti: 3 + 240 + 1024 = 1267.

'4F3' in esadecimale si converte in 1267 in decimale.

Convertiamo 'A2' in esadecimale al suo equivalente decimale:

1. Prendiamo la cifra più a destra, '2', e moltiplichiamo per \(16^0\) (cioè 1). 2 × 1 = 2.
2. Passiamo alla cifra successiva a sinistra, 'A'. 'A' in decimale è 10. Moltiplichiamo per \(16^1\) (cioè 16). 10 × 16 = 160.
3. Sommiamo tutti i risultati ottenuti: 2 + 160 = 162.

'A2' in esadecimale si converte in 162 in decimale.

Convertiamo '3A' in esadecimale al suo equivalente decimale. 'A' rappresenta 10 e '3' rappresenta 3. Usando la notazione posizionale: 3(16^1) + 10(16^0) = 48 + 10 = 58. Quindi, '3A' in decimale è 58.

Perché usare l'esadecimale?

Potresti chiederti: perché dovremmo preoccuparci della notazione esadecimale? La risposta giace nell'informatica e nella rappresentazione dei dati. I computer utilizzano il sistema binario (base-2) per rappresentare e elaborare le informazioni. L'esadecimale fornisce una rappresentazione più concisa dei dati rispetto al binario, rendendolo utile per la programmazione e il debugging.

Il valore binario '101001001' può essere rappresentato come 'A9' in esadecimale. Piuttosto che scrivere nove cifre binarie, possiamo usare solo due caratteri esadecimali, rendendo la lettura e la scrittura dei dati molto più efficienti.

Riepilogo

La notazione esadecimale è un sistema numerico base-16 che utilizza i simboli 0-9 e A-F. Ha applicazioni significative in informatica, dove serve come una forma efficiente per rappresentare dati binari. Comprendere la notazione esadecimale e saper convertire tra decimale ed esadecimale è fondamentale per chiunque lavori nell'ambito della tecnologia.